Alternative stress blocks
General stress blocks
Parabola-rectangles are commonly uses for concrete stress-strain curves.
The parabolic curve can be characterised as
fcf=a(εpε)2+b(εpε)
Define
f′=fcf
and
η=εpε
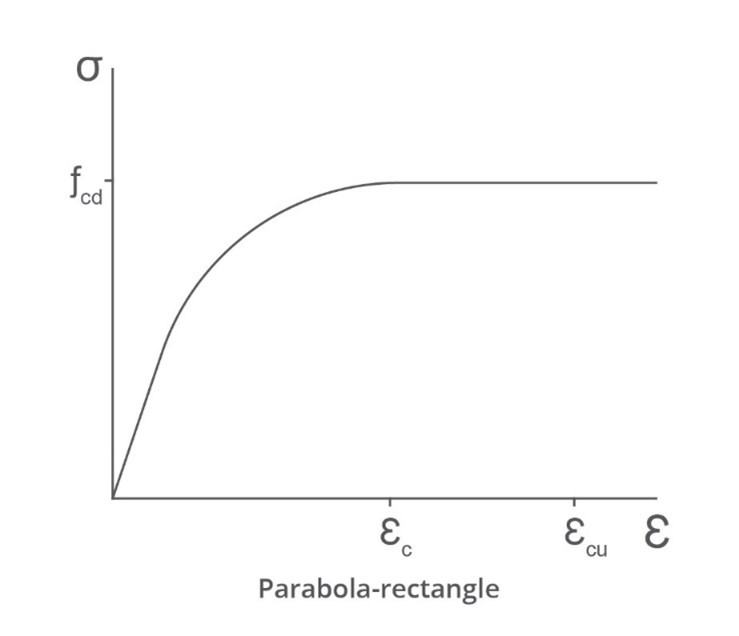
If the curve is taken to be tangent to the plateau then at n=1,f′=1 and dηdf′=0.
Solving for the coefficients gives a=−1 and b=2 so
f′=2η−η2
The area under the curve is given by
Ap=∫01f′dη=[η2−3η3]01=32
For bi-linear curve with the strain transition at εb the area under the curve to εp is
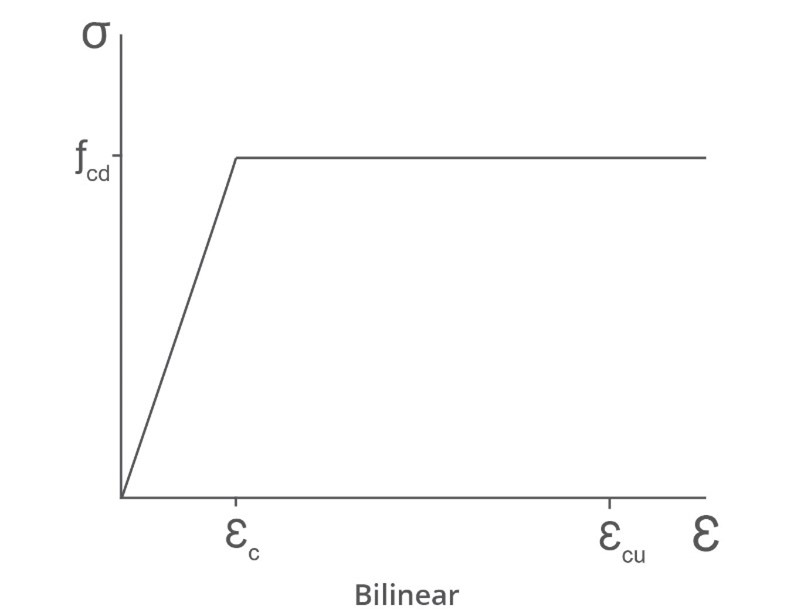
Ab=2ηb+(1−ηb)=1−2ηb
Equating the areas
1−2ηb=32
or
ηb=32
So
εc,b=32εc,p
For a rectangular stress block with the strain transition at εr the area under the curve to εp is
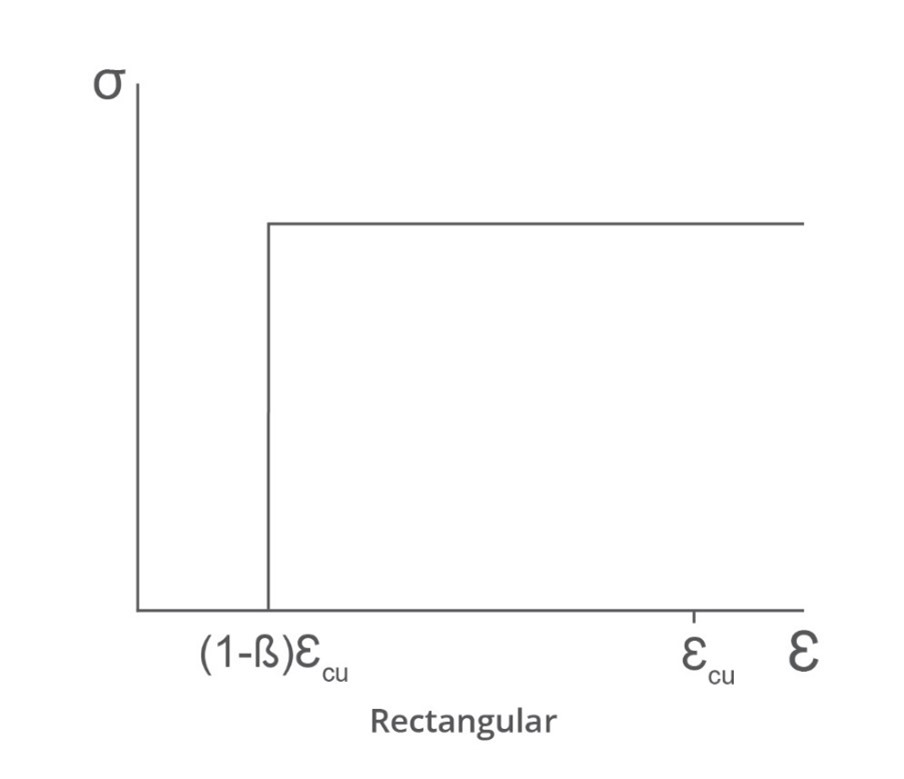
Ab=1−ηr
Equating the areas
1−ηr=32
or
ηr=31
so
εcJ=31εc,p

