Mander and Mander confined curve

The Mander$^1$ curve is available for both strength and serviceability analysis and the Mander confined curve for strength analysis.

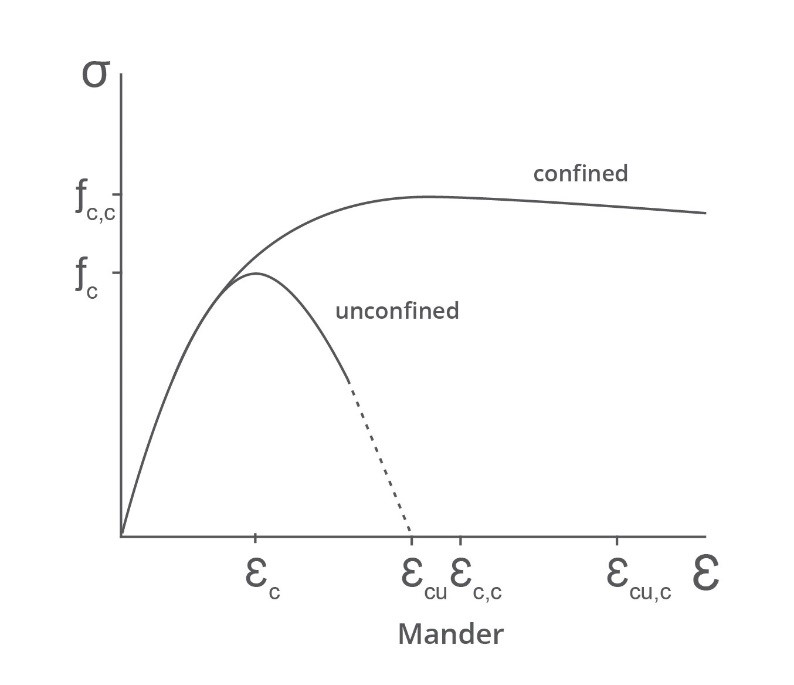
For unconfined concrete, the peak of the stress-strain curve occurs at a stress equal to the unconfined cylinder strength unconfined cylinder strength $f_c$ and strain $\varepsilon_c$ generally taken to be 0.002 . Curve constants are calculated from

$$E_{\sec }=f_c / \varepsilon_c$$

and

$$r=\frac{E}{E-E_{\mathrm{sec}}}$$

Then for strains $0 \leq \varepsilon \leq 2 \varepsilon_c$ the stress $\sigma$ can be calculated from:

$$\sigma=f_c \frac{\eta r}{r-1+\eta^r}$$

where

$$\eta=\frac{\varepsilon}{\varepsilon_c}$$

The curve falls linearly from $\varepsilon_{c} > 2\varepsilon_{co}$ to the spalling strain $\varepsilon_{cu}$. The spalling strain can be taken as 0.005-0.006.

To generate the confined curve the confined strength $f_{c, c}$ must first be calculated. This will depend on the level of confinement that can be achieved by the reinforcement. The maximum strain $\varepsilon_{cu,c}$ also needs to be estimated. This is an iterative calculation, limited by hoop rupture, with possible values ranging from 0.01 to 0.06 . An estimate of the strain could be made from EC2 formula (3.27) above with an upper limit of 0.01 .

The peak strain for the confined curve $\varepsilon_{c,c}$ is given by:

$$\varepsilon_{c,c}=\varepsilon_c\left[1+5\left(\frac{f_{c,c}}{f_c}-1\right)\right]$$

Curve constants are calculated from

$$E_{s e c}=f_{c, c} / \varepsilon_{c, c}$$

and

$$r=\frac{E}{E-E_{\mathrm{sec}}}$$

as before.

$E$ is the tangent modulus of the unconfined curve, given above. Then for strains $0 \leq \varepsilon \leq \varepsilon_{c u s}$ the stress $\sigma$ can be calculated from:

$$\sigma=f_{c, c} \frac{\eta r}{r-1+\eta^\tau}$$

where

$$\eta=\frac{\varepsilon}{\varepsilon_{c, c}}$$

Endnotes

1. Mander J, Priestly M, and Park R. Theoretical stress-strain model for confined concrete. Journal of Structural Engineering, 114(8), pp1804-1826, 1988.