Parabola-rectangles are commonly uses for concrete stress-strain curves.
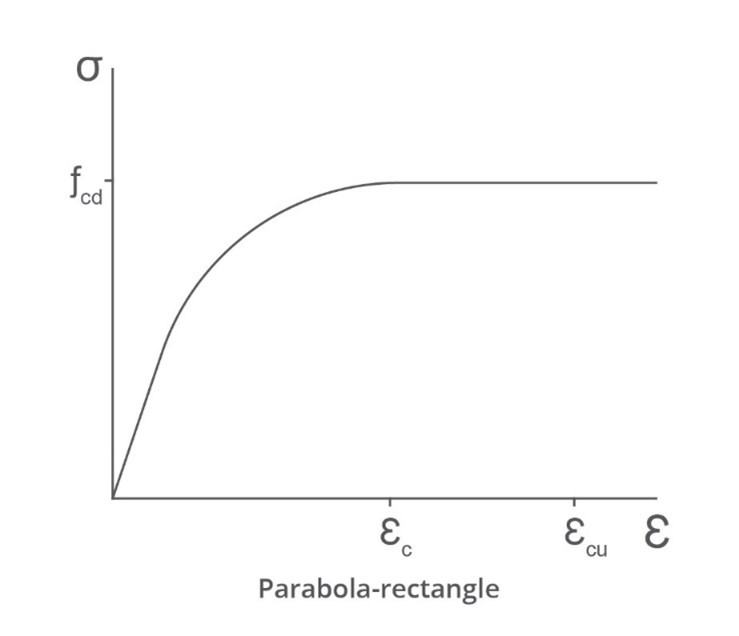
The parabolic curve can be characterised as
fcdf=a(εcε)2+b(εcε)
At strains above εc the stress remains constant. For most design codes the parabola is taken as having zero slope where it meets the horizontal portion of the stress-strain curve.
fcdf=[1−(1−εcε)2]
The Hong Kong Code of Practice (supported by the Hong Kong Institution of Engineers) interpret the curve so that the initial slope is the elastic modulus (meaning that the parabola is not tangent to the horizontal portion of the curve).
fcdf=[1−(EsE)](εcε)2+(EsE)(εcε)
where the secant modulus is
Es=εcfcd
In Eurocode the parabola is modified
fcdf=[1−(1−εcε)n]
and
n=2n=1.4+23.4[(90−fc)/100]4fc≤50MPafc>50MPa 