Park

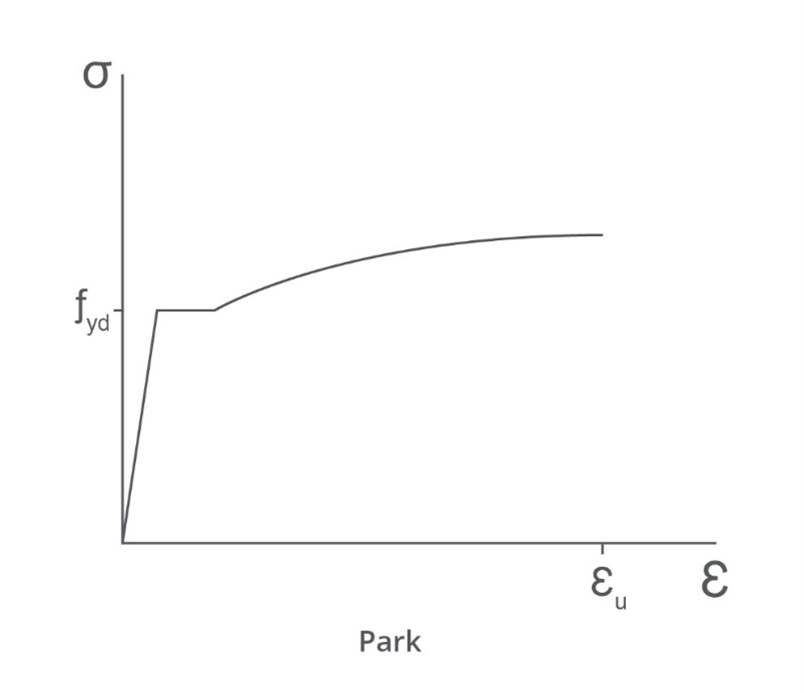
The steel stress-strain curve is characterised a liner response to yield, followed by a fully plastic zone, before hardening until failure. The initial slope is defined by the elastic modulus, $E$, until the stress reaches $f_{yd}$ . The slope is then zero for a short strain range, then rising to a peak stress before failure.

$$\sigma=f_{ud}-(f_{ud}-f_{yd})\Bigl(\frac{\varepsilon_u-\varepsilon}{\varepsilon_u-\varepsilon_p}\Bigl)^P \\$$ $$p=E\Bigl(\frac{\varepsilon_u-\varepsilon_p}{f_{ud}-f_{yd}}\Bigl)$$

The hardening zone can be approximated by a parabola

$$\frac{\sigma}{f_{yd}}=a\varepsilon^2+b\varepsilon+c$$

Defining the perfectly plastic strain limit as $\varepsilon_p$ and assuming zero slope at $\varepsilon_u$ then

$$1=a\varepsilon_p^2+b\varepsilon_p+c$$ $$\frac{f_{ud}}{f_{yd}}=a\varepsilon_u^2+b\varepsilon_u+c$$ $$b=-2a\varepsilon_u$$

The difference between the first two gives

$$\frac{f_{ud}}{f_{yd}}-1=a(\varepsilon_u^2-\varepsilon_p^2)+b(\varepsilon_u-\varepsilon_p)$$

And substituting the third into this gives

$$\frac{f_{ud}}{f_{yd}}-1=a[(\varepsilon_u^2-\varepsilon_p^2)-2\varepsilon_u(\varepsilon_u-\varepsilon_p)]$$

or

$$a=\frac{1-(f_{ud}/f_{yd})}{(\varepsilon_u-\varepsilon_p)^2}$$ $$b=-2\varepsilon_ua$$ $$c=1-b\varepsilon_p-a\varepsilon_p^2$$