Solution

The basic idea behind AdSec is that the state of strain across a section varies linearly and can be defined by a strain plane. As the variation is linear the strain plane can be defined by a scalar axial strain (applied at a specified point) and a curvature vector.

$$\bar{\varepsilon}=\left\lfloor\varepsilon_x, \kappa_y, \kappa_z\right\rfloor \\$$

Then the axial force and moments in the section are then defined as

$$N_x=\int\limits_{A} \sigma(\varepsilon) d A \\$$

$$M_y=\int\limits_{A} \sigma(\varepsilon) z d A \\$$

$$M_z=\int\limits_{A} \sigma(\varepsilon)d A \\$$

This can be characterized in the same way as the strain plane as

$$\bar{N}=\left[N_x, M_y, M_z\right]\\$$

There are many different calculations in AdSec but they are all defined as solution to a set of equations which are functions of the strain plane.

When checking the strength of a section given the axial force and a moment vector, the solution is to find the maximum moment possible before the section fails. There are several criteria to be checked but the primary criteria is

$$N_x=N_{x,app}$$

$$\theta_M=\theta_{M,app}$$

$$\varepsilon_{max}=\varepsilon_u$$

Where $N_x$ is the axial force, $\theta_M$ is the moment angle, $\varepsilon_{max}$ is the maximum strain in the section, $\varepsilon_u$ is the ultimate (failure) strain of the material and the subscript app is for applied.

The basic solution procedure is select an initial trial strain and calculate the target values.

$$N_x=f_1( \overline{\varepsilon})$$

$$\theta_M=f_2( \overline{\varepsilon})$$

$$\varepsilon_{max}=f_3( \overline{\varepsilon})$$

The solution is then iterative until a converged solution for the criteria above is achieved. Once this strain plane is found the ultimate moment $M_u$ is the moment from integrating the final strain plane.

Solver Solution Space

Any particular load condition can be considered as a point in the $(N,M_{yy},M_{zz})$ space. It is them possible to construct a failure envelope -- this can be for ULS strength or for a serviceability criteria, such as cracking. The failure envelope is then typically an onion shape with axial force as the vertical axis. Any point inside the space represent a valid force state, but a point outside the surface has failed.

The analysis is then concerned with determining the force position with respect to the failure surface. In a ULS analysis the solution holds the axial force constant and find the ratio of the applied moment to the moment corresponding to the projection on to the failure surface.

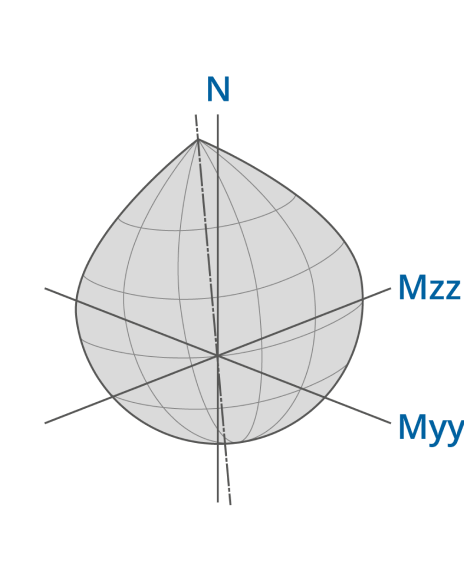
Similarly, the chart options N/M corresponds to a vertical slice through the onion and a horizontal slice corresponds to an $M_{yy}/M_{zz}$ chart.

Solver Search Process

The solution is iterative and assumes plane sections remain plane. The iteration searches through possible strain planes. Strain $\varepsilon$ at point $(y,z)$ is $\varepsilon_x+\kappa_{zy}+\kappa_{yz}$. For each strain plane: locked in strains are added, stresses are calculated from the non-linear material curves, forces and moments are calculated by integration of stresses over the section, the three search conditions are then checked.

Analysis	Condition 1	Condition 2	Condition 3
ULS : Strength	Axial force	Moment angle	Ultimate strain
ULS : N/M charts	Moment angle	Strain condition	Ultimate strain
SLS & ULS : Loads	Axial force	Moment angle	Applied moment
SLS : Cracking	Axial force	Moment angle	Cracking strain moment

The iteration continues until the three variables $\varepsilon_x,\kappa_z,\kappa_y$ are found with form a strain plane $\widehat{\varepsilon}$ that satisfies the (up to) three conditions.

SLS and ULS loads analysis

For a loads analysis AdSec searches for a strain plane which satisfies:

• axial force = applied axial force

• moment = applied moment

• moment angle = applied moment angle